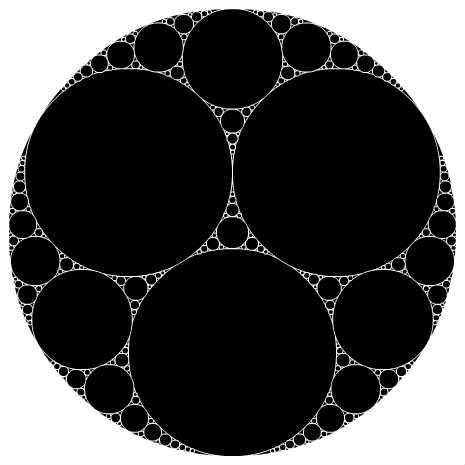
アポロニウスのガスケット Apollonian Gasket (2)
forked from アポロニウスのガスケット Apollonian Gasket (1) (diff: 16)
ActionScript3 source code
/**
* Copyright Aquioux ( http://wonderfl.net/user/Aquioux )
* MIT License ( http://www.opensource.org/licenses/mit-license.php )
* Downloaded from: http://wonderfl.net/c/xZ8z
*/
// forked from Aquioux's アポロニウスのガスケット Apollonian Gasket (1)
package {
//import aquioux.math.Complex;
import flash.display.Graphics;
import flash.display.Shape;
import flash.display.Sprite;
[SWF(width = "465", height = "465", frameRate = "30", backgroundColor = "#ffffff")]
/**
* アポロニウスのガスケット(2)
* 3つの正接円の内接円周辺に円を敷き詰める
* @see http://aquioux.net/blog/?p=3825
* @author YOSHIDA, Akio
*/
public class Main extends Sprite {
// 再帰の終了判定(描画円の半径の最小値)
static private const MIN_RADIUS:Number = 1.75;
// キャンバス
private var canvas_:Shape;
// 背景色
static private const FILL_COLOR:uint = 0xffffff;
// 円の色
static private const CIRCLE_COLOR:uint = 0x000000;
/**
* コンストラクタ
*/
public function Main() {
// サイズ
const CENTER_X:Number = stage.stageWidth / 2;
const CENTER_Y:Number = stage.stageHeight / 2;
const SHIFT_X:int = -1000;
const SHIFT_Y:int = -1000;
// キャンバス
canvas_ = new Shape();
canvas_.x = SHIFT_X;
canvas_.y = SHIFT_Y;
addChild(canvas_);
// 正接円の極座標計算
var radianA:Number = 90 * Math.PI / 180;
var radianB:Number = 210 * Math.PI / 180;
var radianC:Number = 330 * Math.PI / 180;
const LENGTH:int = stage.stageWidth * 0.26 >> 0;
// 正接円の生成
var circleA:Circle = new Circle(new Complex(CENTER_X + Math.cos(radianA) * LENGTH - SHIFT_X, CENTER_Y + Math.sin(radianA) * LENGTH - SHIFT_Y), 0);
var circleB:Circle = new Circle(new Complex(CENTER_X + Math.cos(radianB) * LENGTH - SHIFT_X, CENTER_Y + Math.sin(radianB) * LENGTH - SHIFT_Y), 0);
var circleC:Circle = new Circle(new Complex(CENTER_X + Math.cos(radianC) * LENGTH - SHIFT_X, CENTER_Y + Math.sin(radianC) * LENGTH - SHIFT_Y), 0);
Calculator.calcTangentCircles(circleA, circleB, circleC);
// 外接円の生成
var outer:Circle = Calculator.calcSoddyCircles(circleA, circleB, circleC, false);
// 外接円の描画
drawCircle(outer, CIRCLE_COLOR);
// 正接円の描画
drawCircle(circleA, CIRCLE_COLOR);
drawCircle(circleB, CIRCLE_COLOR);
drawCircle(circleC, CIRCLE_COLOR);
// 内接円の生成と描画(再帰処理)
drawInnerCircles(circleA, circleB, circleC); // 3つの正接円
drawInnerCircles(circleA, circleB, outer); // 2つの正接円と外接円その1
drawInnerCircles(circleB, circleC, outer); // 2つの正接円と外接円その2
drawInnerCircles(circleC, circleA, outer); // 2つの正接円と外接円その3
}
// 内接円の生成と描画(再帰処理)
private function drawInnerCircles(circleA:Circle, circleB:Circle, circleC:Circle):void {
// 内接円の生成
var inner:Circle = Calculator.calcSoddyCircles(circleA, circleB, circleC);
// 終了判定
if (inner.radius < MIN_RADIUS) return;
// 内接円の描画
drawCircle(inner, CIRCLE_COLOR);
// 3分木で再帰
drawInnerCircles(circleA, circleB, inner);
drawInnerCircles(circleB, circleC, inner);
drawInnerCircles(circleC, circleA, inner);
}
// 描画
private function drawCircle(circle:Circle, color:uint = 0x0):void {
var g:Graphics = canvas_.graphics;
g.lineStyle(0, FILL_COLOR);
g.beginFill(color);
g.drawCircle(circle.center.x, circle.center.y, circle.radius);
g.endFill();
}
}
}
//package {
//import aquioux.math.Complex;
//import aquioux.math.ComplexMath;
/**
* 「デカルトの円定理」あるいは "Soddy Circles"
* http://en.wikipedia.org/wiki/Descartes'_theorem
* http://mathworld.wolfram.com/DescartesCircleTheorem.html
* http://mathworld.wolfram.com/SoddyCircles.html
* http://mathworld.wolfram.com/InnerSoddyCircle.html
* http://mathworld.wolfram.com/OuterSoddyCircle.html
* @author YOSHIDA, Akio
*/
/*public*/ class Calculator {
/**
* 3つの正接円の中心座標からそれぞれの半径を算出
* @param circleA
* @param circleB
* @param circleC
*/
static public function calcTangentCircles(circleA:Circle, circleB:Circle, circleC:Circle):void {
// 2つの正接円間の距離(2つの正接円の半径の和)を算出
var distAB:Number = dist(circleA.center, circleB.center); // = circleA.radius + circleB.radius
var distBC:Number = dist(circleB.center, circleC.center); // = circleB.radius + circleC.radius
var distCA:Number = dist(circleC.center, circleA.center); // = circleC.radius + circleA.radius
// 各正接円の半径を算出
circleA.radius = (distCA + distAB - distBC) / 2;
circleB.radius = (distAB + distBC - distCA) / 2;
circleC.radius = (distBC + distCA - distAB) / 2;
}
// 2つの複素数間の距離を求める
static private function dist(center1:Complex, center2:Complex):Number {
return ComplexMath.abs(ComplexMath.subtract(center1, center2));
}
/**
* 3つの正接円から、その内接円もしくは外接円の半径と中心座標を算出
* @param circleA
* @param circleB
* @param circleC
* @param isInner 3つの内接円の内接円を求めるのか、外接円を求めるのか。true:内接円、false:外接円
* @return
*/
static public function calcSoddyCircles(circleA:Circle, circleB:Circle, circleC:Circle, isInner:Boolean = true):Circle {
// ----- 4番目の円の半径を求める -----
// 4番目の円の曲率kを求める公式
// (k1 + k2 + k3 + k4)^2 = 2 * (k1^2 + k2^2 + k3^2 + k4^2)
// ↓
// k4 = k1 + k2 + k3 ± 2 * √(k1*k2 + k2*k3 + k3*k1)
// 各正接円の曲率
var kA:Number = 1 / circleA.radius; // k1
var kB:Number = 1 / circleB.radius; // k2
var kC:Number = 1 / circleC.radius; // k3
// ±前の部分
var kABC:Number = kA + kB + kC; // k1 + k2 + k3
// ±後の部分
var kAB:Number = kA * kB; // k1 * k2
var kBC:Number = kB * kC; // k2 * k3
var kCA:Number = kC * kA; // k3 * k1
var sq1:Number = 2 * Math.sqrt(kAB + kBC + kCA); // 2 * √(k1*k2 + k2*k3 + k3*k1)
// k4 の計算結果(逆数にして半径に)
if (!isInner) sq1 = -sq1; // 外接円の場合
var radiusD:Number = 1 / (kABC + sq1);
// ----- 4番目の円の中心座標を求める -----
// 4番目の円の中心座標(複素平面上)を求める公式
// (z1*k1 + z2*k2 + z3*k3 + z4*k4)^2 = 2 * (z1^2*k1^2 + z2^2*k2^2 + z3^2*k3^2 + z4^2*k4^2)
// ↓
// z4 = (z1*k1 + z2*k2 + z3*k3 ± 2 * √(z1*k1 * z2*k2 + z2*k2 * z3*k3 + z3*k3 * z1*k1)) / k4
// 分子のうち、±前の部分
var zkA:Complex = ComplexMath.scale(circleA.center, kA); // z1 * k1
var zkB:Complex = ComplexMath.scale(circleB.center, kB); // z2 * k2
var zkC:Complex = ComplexMath.scale(circleC.center, kC); // z3 * k3
var zkABC:Complex = ComplexMath.add(ComplexMath.add(zkA, zkB), zkC);
// z1*k1 + z2*k2 + z3*k3
// 分子のうち、±後の部分
var zkAB:Complex = ComplexMath.multiply(zkA, zkB); // z1*k1 * z2*k2
var zkBC:Complex = ComplexMath.multiply(zkB, zkC); // z2*k2 * z3*k3
var zkCA:Complex = ComplexMath.multiply(zkC, zkA); // z3*k3 * z1*k1
var zkAABBCC:Complex = ComplexMath.add(ComplexMath.add(zkAB, zkBC), zkCA);
// z1*k1 * z2*k2 + z2*k2 * z3*k3 + z3*k3 * z1*k1
var sq2:Complex = ComplexMath.scale(ComplexMath.pow(zkAABBCC, 1 / 2), 2);
// 2 * √(z1*k1 * z2*k2 + z2*k2 * z3*k3 + z3*k3 * z1*k1)
// z4 の計算結果
if (!isInner) sq2 = ComplexMath.scale(sq2, -1); // 外接円の場合
var zD:Complex = ComplexMath.scale(ComplexMath.add(zkABC, sq2), radiusD);
return new Circle(zD, radiusD);
}
}
//}
//package {
//import aquioux.math.Complex;
/**
* 円クラス
* @author YOSHIDA, Akio
*/
/*public*/ class Circle {
/**
* 中心座標
*/
public function get center():Complex { return _center; }
public function set center(value:Complex):void { _center = value; }
private var _center:Complex;
/**
* 半径
*/
public function get radius():Number { return _radius; }
public function set radius(value:Number):void { _radius = value; }
private var _radius:Number;
/**
* コンストラクタ
* @param center 中心座標
* @param radius 半径
*/
public function Circle(center:Complex, radius:Number) {
_center = center;
_radius = radius;
}
}
//}
//package aquioux.math {
/**
* 複素数
* @author YOSHIDA, Akio
*/
/*public*/ final class Complex {
/**
* 実数部
*/
// 実数
public function get real():Number { return _real; }
public function set real(value:Number):void { _real = value; }
// 直交座標におけるX座標
public function get x():Number { return _real; }
public function set x(value:Number):void { _real = value; }
// 局座標における長さ
public function get length():Number { return _real; }
public function set length(value:Number):void { _real = value; }
// 実数部
private var _real:Number;
/**
* 数部
*/
// 虚数
public function get imag():Number { return _imag; }
public function set imag(value:Number):void { _imag = value; }
// 直交座標におけるY座標
public function get y():Number { return _imag; }
public function set y(value:Number):void { _imag = value; }
// 局座標における偏角
public function get angle():Number { return _imag; }
public function set angle(value:Number):void { _imag = value; }
// 虚数部
private var _imag:Number;
/**
* コンストラクタ
* @param real 実数部
* @param imag 虚数部
*/
public function Complex(real:Number = 0.0, imag:Number = 0.0) {
_real = real;
_imag = imag;
}
/**
* 複製
* @return 複製した複素数
*/
public function clone():Complex {
return new Complex(_real, _imag);
}
/**
* toString
* @return 文字列表示
*/
public function toString():String {
return String(_real) + " + " + String(_imag) + " i";
}
}
//}
//package aquioux.math {
/**
* 複素数の定数と演算
* @author YOSHIDA, Akio
*/
/*public*/ final class ComplexMath {
// ----- 定数 -----
/**
* ゼロ
*/
static public const ZERO:Complex = new Complex(0.0, 0.0);
/**
* 純実数1
*/
static public const PURE_REAL:Complex = new Complex(1.0, 0.0);
/**
* 純虚数i
*/
static public const PURE_IMAGINARY:Complex = new Complex(0.0, 1.0);
/**
* 加算
* @param a 加算項1
* @param b 加算項2
* @return 加算結果
*/
static public function add(a:Complex, b:Complex):Complex {
return new Complex(
a.real + b.real,
a.imag + b.imag
);
}
/**
* 減算
* @param a 減算項1
* @param b 減算項2
* @return 減算結果
*/
static public function subtract(a:Complex, b:Complex):Complex {
return new Complex(
a.real - b.real,
a.imag - b.imag
);
}
/**
* 乗算
* @param a 乗算項1
* @param b 乗算項2
* @return 乗算結果
*/
static public function multiply(a:Complex, b:Complex):Complex {
var aRl:Number = a.real;
var aIm:Number = a.imag;
var bRl:Number = b.real;
var bIm:Number = b.imag;
return new Complex(
aRl * bRl - aIm * bIm,
aRl * bIm + aIm * bRl
);
}
/**
* 除算
* @param a 除算項1
* @param b 除算項2
* @return 除算結果
*/
static public function divide(a:Complex, b:Complex):Complex {
return multiply(a, reciprocal(b));
}
/**
* スケーリング(第2引数が実数である乗算)
* @param c 複素数
* @param n 実数
* @return 乗算結果
*/
static public function scale(c:Complex, n:Number):Complex {
return new Complex(
c.real * n,
c.imag * n
);
}
/**
* 絶対値の2乗
* @param c 複素数
* @return 絶対値の2乗
*/
// c * c~ = c.real^2 + c.imag^2
static public function absSquare(c:Complex):Number {
var rl:Number = c.real;
var im:Number = c.imag;
return rl * rl + im * im;
}
/**
* 絶対値(=長さ)
* @param c 複素数
* @return 絶対値
*/
// |c| = √(c * c~) = √(c.real^2 + c.imag^2)
static public function abs(c:Complex):Number {
return Math.sqrt(absSquare(c));
}
/**
* 共役複素数
* @param c 複素数
* @return 共役複素数
*/
static public function conjugate(c:Complex):Complex {
return new Complex(
c.real,
-c.imag
);
}
/**
* 逆数
* @param c 複素数
* @return 逆数
*/
static public function reciprocal(c:Complex):Complex {
var val:Number = absSquare(c);
return new Complex(
c.real / val,
-c.imag / val
);
}
/**
* 冪乗
* @param c 複素数
* @param exponent 冪指数
* @return 冪乗結果
*/
static public function pow(c:Complex, exponent:Number):Complex {
// 極座標形式で計算
var cc:Complex = cartesianToPolar(c);
var length:Number = Math.pow(cc.length, exponent);
var angle:Number = cc.angle * exponent;
return new Complex(
length * Math.cos(angle),
length * Math.sin(angle)
);
}
/**
* 直交座標形式から極座標形式へ
* @param c 直交座標形式の複素数
* @return 極座標形式の複素数
*/
// 対数関数との関連性
static public function cartesianToPolar(c:Complex):Complex {
var cc:Complex = new Complex();
cc.length = abs(c); // 長さ
cc.angle = Math.atan2(c.imag, c.real); // 偏角
return cc;
}
/**
* 極座標形式から直交座標形式へ
* @param c 極座標形式の複素数
* @return 直交座標形式の複素数
*/
// 指数関数との関連性
static public function polarToCartesian(c:Complex):Complex {
var length:Number = c.length;
var angle:Number = c.angle;
return new Complex(
length * Math.cos(angle),
length * Math.sin(angle)
);
}
/**
* 対数関数
* @param c 複素数
* @return 対数値
*/
// 実数部は絶対値、虚数部は偏角
static public function log(c:Complex):Complex {
var cc:Complex = cartesianToPolar(c);
return new Complex(
Math.log(cc.length),
cc.angle
);
}
/**
* 指数関数
* @param c 複素数
* @return 指数値
*/
// e^length * (cos(angle) + sin(angle)i)
static public function exp(c:Complex):Complex {
var val:Number = Math.exp(c.real);
var im:Number = c.imag;
return new Complex(
val * Math.cos(im),
val * Math.sin(im)
);
}
}
//}