forked from: Mt. Fuji
forked from Mt. Fuji (diff: 10)
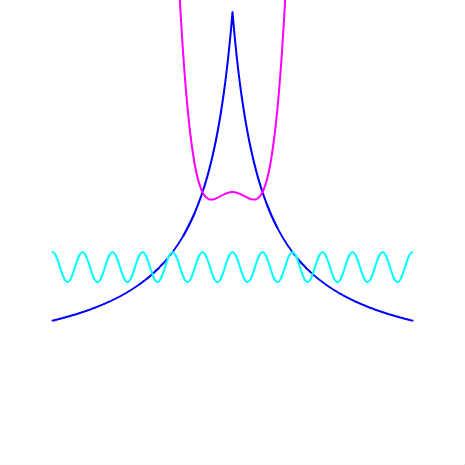
f(x)= x^4-x^2+6, 12/(|x|+1), g(x)= 1/2*cos(2πx)+7/2 _____ 式の解説は[FumioNonaka.com Newsletter: no.109]「スクリプト&数学覚え書き」 http://archive.mag2.com/0000118977/20130105115435000.html
ActionScript3 source code
/**
* Copyright Fumio ( http://wonderfl.net/user/Fumio )
* MIT License ( http://www.opensource.org/licenses/mit-license.php )
* Downloaded from: http://wonderfl.net/c/svB9
*/
// forked from Fumio's Mt. Fuji
// f(x)= x^4-x^2+6 (|x|<=1), 12/(|x|+1) (|x|>1), g(x)= 1/2*cos(2x)+7/2 (|x|<=2)
package {
import flash.display.Sprite;
import flash.display.Graphics;
public class MtFuji extends Sprite {
private var minX:Number = -6;
private var maxX:Number = 6;
private var increments:Number = 0.05;
private var originX:Number = stage.stageWidth / 2;
private var originY:Number = stage.stageHeight * 0.8;
private var scale:Number = 30;
private var myGraphics:Graphics = graphics;
public function MtFuji() {
drawGraph();
}
private function drawGraph():void {
var x:Number;
var y:Number;
var start:uint = 1;
myGraphics.lineStyle(2, 0x0000FF);
for (x = minX; x < maxX; x += increments) {
y = f2(x);
drawLine(x, y, start);
start &= 0;
}
start = 1;
myGraphics.lineStyle(2, 0xFF00FF);
for (x = minX; x < maxX; x += increments) {
y = f(x);
drawLine(x, y, start);
start &= 0;
}
start = 1;
myGraphics.lineStyle(2, 0x00FFFF);
for (x = minX; x < maxX; x += increments) {
y = g(x);
drawLine(x, y, start);
start &= 0;
}
}
// f(x) = x^4 - x^2 + 6 (|x|<=1)
private function f(x:Number):Number {
return Math.pow(x, 4) - Math.pow(x, 2) + 6;
}
// 12 / (|x| + 1) (|x|>1)
private function f2(x:Number):Number {
return 12 / (Math.abs(x) + 1);
}
// g(x) = 1/2 * cos(2πx) + 7/2 (|x|<=2)
private function g(x:Number):Number {
return 1 / 2 * Math.cos(2 * Math.PI * x) + 7 / 2;
}
private function drawLine(x:Number, y:Number, moveTo:uint):void {
x = originX + x * scale;
y = originY - y * scale;
if (moveTo) {
myGraphics.moveTo(x, y);
} else {
myGraphics.lineTo(x, y);
}
}
}
}